Goal:

Compute several direction with the AD forward mode to create the Jacobian.
Evaluate the reverse tape multiple times to compute the Jacobian.

Prerequisite: Tutorial 1 - Forward mode AD, Tutorial 2 - Reverse mode AD

Function: Simple vector valued function

template<typename Real>
void func(const Real* x, size_t l, Real* y) {
  y[0] = 0.0;
  y[1] = 1.0;
  for(size_t i = 0; i < l; ++i) {
    y[0] += x[i];
    y[1] *= x[i];
  }
}
 

Full code:

 
#include <codi.hpp>
#include <iostream>
 
template<typename Real>
void func(const Real* x, size_t l, Real* y) {
  y[0] = 0.0;
  y[1] = 1.0;
  for(size_t i = 0; i < l; ++i) {
    y[0] += x[i];
    y[1] *= x[i];
  }
}
 
 
void forwardModeJacobianComputation() {
 
  using Real = codi::RealForward;
 
  Real x[5];
  Real y[2];
  x[0] = 1.0;
  x[1] = 2.0;
  x[2] = 3.0;
  x[3] = 4.0;
  x[4] = 5.0;
 
  codi::Jacobian<double> jacobian(2,5);
 
  // Step 1: Iterate over the input dimension
  for(size_t i = 0; i < 5; ++i) {
    x[i].gradient() = 1.0; // Step 2: Set the seeding for the i-th input variable
 
    func(x, 5, y);  // Step 3: Evaluate the function
 
    // Step 3: Get the gradients from the outputs.
    for(size_t j = 0; j < 2; ++j) {
      jacobian(j,i) = y[j].getGradient();
    }
 
    x[i].gradient() = 0.0; // Step 4: Reset the seeding for the i-th input variable
  }
 
  std::cout << "Forward mode Jacobian:" << std::endl;
  std::cout << "f(1 .. 5) = (" << y[0] << ", " << y[1] << ")" << std::endl;
  std::cout << "df/dx (1 .. 5) = \n" << jacobian << std::endl;
}
 
void reverseModeJacobianComputation() {
 
  using Real = codi::RealReverse;
  using Tape = typename Real::Tape;
 
  Real x[5];
  Real y[2];
  x[0] = 1.0;
  x[1] = 2.0;
  x[2] = 3.0;
  x[3] = 4.0;
  x[4] = 5.0;
 
  codi::Jacobian<double> jacobian(2,5);
 
  Tape& tape = Real::getTape();
  tape.setActive();
 
  // Step 1: Record the tape
  for(size_t i = 0; i < 5; ++i) {
    tape.registerInput(x[i]);
  }
 
  func(x, 5, y);
 
  tape.registerOutput(y[0]);
  tape.registerOutput(y[1]);
 
  tape.setPassive();
 
  // Step 2: Iterate over the output dimension
  for(size_t i = 0; i < 2; ++i) {
    y[i].gradient() = 1.0; // Step 3: Set the seeding for the i-th output variable
 
    tape.evaluate();
 
    // Step 4: Get the gradients from the inputs.
    for(size_t j = 0; j < 5; ++j) {
      jacobian(i, j) = x[j].getGradient();
    }
 
    tape.clearAdjoints(); // Step 5: Clear the adjoints
  }
 
  std::cout << "Reverse mode Jacobian:" << std::endl;
  std::cout << "f(1 .. 5) = (" << y[0] << ", " << y[1] << ")" << std::endl;
  std::cout << "df/dx (1 .. 5) = \n" << jacobian << std::endl;
 
  tape.reset(false);
}
 
int main(int nargs, char** args) {
  forwardModeJacobianComputation();
 
  std::cout << std::endl;
 
  reverseModeJacobianComputation();
 
  return 0;
}
 

With the forward and reverse AD modes only directional derivatives or reverse directional derivatives can be computed. For a computation of the full Jacobian matrix 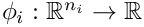$\frac{\d f}{\d x}$ the tangent direction $\dot x$ or adjoint direction $\bar y$ need to be set to the unit vectors and the corresponding AD mode has to be evaluated for each unit vector.

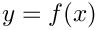
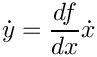
In general, the Jacobian computation for both modes, forward and reverse, uses all things that have been explained in the basic tutorials.

Forward mode

For a Jacobian evaluation in the forward mode an iteration over the input dimension is required (Step 1). Then a regular forwad mode evaluation follows (Step 2 and Step 3). The new element is Step 4. Here, the tangent seeding from Step 1 is cleared so that only unit vectors are set as tangent direction.

Reverse mode

The Jacobian evaluation in the reverse mode differs a little bit form the procedure in Tutorial 2 - Reverse mode AD. The tape is recorded as usual, but only once (Step 1). Afterwards, a regular seeding of the output values is performed and the tape is evaluated (Step 3 and Step 4). The additional function call is required in Step 5. Here, the adjoint vector of CoDiPack is cleared, such that no adjoint values from the previous tape evaluation disturb the result. The function clearAdjoints only clears the adjoint in contrast to a tape reset which also clears the tape data. The optional parameter on the tape reset function allows to skip the clear of the adjoints.

Performance improvement

CoDiPack clears the adjoints of all intermediate variables automatically, only the ones from input variables are left in place. (Adjoints of output variables are also cleared.) Therefore a complete reset of the adjoint vector is not necessary. After the adjoint of an output value is accessed, the adjoint value can be cleared manually with x[j].gradient() = 0.0 in Step 4. Then Step 5 is no longer necessary. If not all input variables are cleared this way, subsequent results will be wrong.