The introduction given in AD theory and mathematical definitions is formulated in terms of elemental operations. In the view of Statement level recording (Expression templates), let

$w=\phi(u)$

denote a statement in the code where 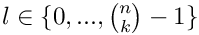$\phi$ is composed of multiple elementary operations and is the vector of arguments.

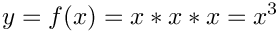
CoDiPack has to evaluate the reverse AD mode for each statement. The equation is:

$\bar u \aeq \frac{d\phi}{du}^T \bar w; \quad \bar w = 0$

Note that 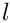$\bar u$ is a vector, too, with the same size as . To enable this evaluation, different taping strategies store different data and have therefore different advantages and disadvantages.

Jacobian taping approach

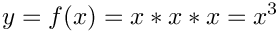
The Jacobian taping approach uses the property that in the above reverse AD equation only $\bar w$ is unknown. The gradient $\frac{d\phi}{du}$ can be computed at the time when the statement is evaluated. The memory consumption is then 5 byte per statement, that is, one byte for the number of arguments and 4 bytes for the left hand side identifier (the identifier of $\bar w$ ). The memory for each argument is 12 bytes, that is, 8 bytes for the Jacobian value and 4 bytes for the identifier of the argument (the identifiers of the components of $\bar u$ ).

This taping approach has multiple advantages:

Jacobians of passive arguments do not need to be stored.
The tape evaluation is very simple (only fused multiply add operations).
Simple implementation.

The disadvantages are:

No primal reevaluation of the tape.
High memory requirement per argument.

Primal value taping approach

The primal value taping approach implements the more traditional taping strategy of AD. It stores all primal values of the computation, such that these values are available during the reverse interpretation. It is important that this is done in a way such that each primal value is only stored once. In the example:

a = ...;
b = a + a;
c = a * a;
d = sin(a);
e = cos(a);

a is used 6 times as an argument and is assigned only once. If the primal value taping approach would store each argument of an operation, then the value of a would be stored 6 times in the above case. The strategy can be shifted such that the value of a is only stored once during the assignment. During the reverse run, the place where the value of a is stored can be accessed through the identifier of a.

If this scheme is used, then for each statement 21 bytes are required. 8 bytes are used for the primal value of the result ( 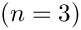), 4 bytes for the identifier (the identifier of $\bar w$ ), 1 byte for the number of passive arguments and 8 bytes for the function pointer to the evaluation procedure. Since CoDiPack uses statement level taping, the number of possible expressions is very large and cannot be covered in a simple enumerator. It is therefore necessary to generate a function for each statement that performs the reverse evaluation. The byte for the number of passive arguments is required because of the activity tracking CoDiPack performs. Each passive value has the identifier zero and therefore the primal value cannot be accessed with this identifier. Consequently, each passive value needs to be stored and since this is a runtime information, the count for each statement needs to be stored, too.

The memory for each argument is then only 4 bytes for the identifier of this argument. This identifier is used to access the adjoint values (components of $\bar u$ ) and the primal value ( ).

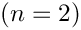
This taping approach has the following advantages:

Low memory for each argument.
Primal reevaluation possible.

The disadvantages are:

Storing of passive values required (8 bytes per argument).
Storing of constant values required (8 bytes per argument).
Function pointer calls in the reverse interpretation.

Comparison

In theory the primal value taping approach should be more efficient than the Jacobian taping approach. If the tape has on average 4 arguments per statement, then the primal value taping approach requires 37 bytes per statement whereas the Jacobian taping approach requires 53 bytes. This would provide a memory reduction of 30%. The problem is that the additional memory requirements for the passive and constant values of the primal value taping approach usually use up the memory savings. It can therefore never be said which taping approach is the better one since it depends on the application and the actual computation.