The expressions in CoDiPack help to perform operations on the statement level instead of the operator level. In an operator overloading framework, the general design of the overloads is like
![\[ \text{Real} \circ \text{Real} \rightarrow \text{Real},
\]](../../form_131.png)
where 



![\[ \text{Expr}_A \circ \text{Expr}_B \rightarrow \text{Expr}_{A \circ B}.
\]](../../form_136.png)
The final return value is now an expression which contains information about the operation, which is indicated by the suffix 
This allows us to move from the differentiation of single elemental operations to the differentiation of full statements with right hand sides that are composed of multiple elemental operations.
On the equation
![\[ w = ((a + b) * (c - d))^2
\]](../../form_138.png)
the pure operator overloading approach would create three intermediate statements

The expression template approach creates one large expression that is represented by the structure
![\[ \text{SQUARE} < \text{MULT} < \text{ADD} < \text{Real}, \text{Real}>, \text{SUB}<\text{Real}, \text{Real}> > > \eqdot
\]](../../form_140.png)
It can be used to evaluate the result 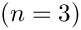
getValue which evaluates the expression. For all other operations the traversal logic classes have to be used.
The current most used expression implementation are:
Custom operations on expressions in CoDiPack are all implemented with the TraversalLogic or CompileTimeTraversalLogic classes. The first one enables custom logic in a runtime context. Variables and results can be stored in the implementation. The CompileTimeTraversalLogic allows for the computation of results in a compile time context. Both classes contain functions for the visit of links, nodes and leaves in the expression graph. The terms are explained in the following picture:
Nodes in the traversal logic are all intermediate operations and leaves are the values on which the operations are evalauted. Links indicate the relations between nodes. Child nodes serve as arguments to their respective parent node.
The graph is traversed with a depth-first search (DFS). On each node the first link is visited, followed by the child of the link. Recursively, the child visits all links and so on. The above example would have the following walk:
Information can be provided or stored in the implementation or propagated via the arguments of the function calls. The default implementation forwards all arguments from the initial call.
Specializations for some common use cases are available:
The CompileTimeTraversalLogic works in the same way as the TraversalLogic and results mostly in the same order of calls. The only difference is that binary expressions perform a reduction of the results from the two children.